Expanding on my 'recent' (haven't blogged in ages admittedly) post about different views in algebra, I have been looking at the idea of showing different expressions using diagrammatic views of sequences, and thought I would outline a few thoughts here:
1) Linear or quadratic?
A really nice thing to do with pupils is to look at patterns that arise from (or generate depending on your point of view) linear sequences, compared to quadratic. In particular what is the difference between the way a linear pattern grows, compared to a quadratic pattern? Have a look at these patterns and see if you can decide whether they show linear or quadratic sequences without writing down the numbers:
It shouldn't be too hard to show pupils that the calculations for the number of squares in each successive pattern is 4 x 2, then 4 x 3, then 4 x 4 then 4 x 5, so in general 4(n+1). Consider the same picture with some slightly different colouring:
and we should be able to demonstrate that this is also 4n + 4 (the yellow squares given by 4n, and then 4 green squares on the end of each pattern). This is also true in quadratic sequences, taking sequence 2 from above:
Similar to above, the calculations this time are 1 x 2, 2 x 3, 3 x 4, 4 x 5, or in general n(n+1), if we then compare to the image below:
We can show quite clearly that this is also n2 + n.
I am sure there are other uses I haven't yet thought of (I think it may be applicable to geometric and Fibonacci sequences as well, and possibly series at A-Level). When I get chance to explore more I will try and remember to write about it!
P.S. - of course if you have multi-link cubes or similar then pupils can actually build these sequences, graphs etc. as well as just seeing or drawing the pictures.
1) Linear or quadratic?
A really nice thing to do with pupils is to look at patterns that arise from (or generate depending on your point of view) linear sequences, compared to quadratic. In particular what is the difference between the way a linear pattern grows, compared to a quadratic pattern? Have a look at these patterns and see if you can decide whether they show linear or quadratic sequences without writing down the numbers:
Most people that know about sequences will be able to identify that the 1st, 3rd and 4th sequences are linear, because the same number of squares are added each time (the colours make this quite easy to identify), whereas in the second and third there are more squares of each colour - what is interesting though is to explore these views of the different sequences:
Linear
Each of the sequences 1, 3, and 4 can be rearranged to give these lines, , showing that they only grow in a 'linear' fashion, which doesn't work with the quadratic sequences as the number of squares is different each time (although you can technically rearrange them to make lines, they don't grow in a linear way).
Another interesting way to look at the linear sequences is using a graph:
Quadratic
Or if you prefer:
What is nice here is that these sequences illustrate that quadratic sequences are the two dimensional extension to linear sequences. The graphs can also be used to illustrate the difference to a quadratic and the quadratic shape:
Showing the curved nature of the quadratic graph as opposed to the straight line nature of a linear graph.
2) Different forms of an expression
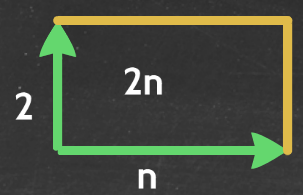
Another possible use of these pictures is to illustrate the different ways of writing identical expressions, for example if we take sequence 1 from above without the colours:
and we should be able to demonstrate that this is also 4n + 4 (the yellow squares given by 4n, and then 4 green squares on the end of each pattern). This is also true in quadratic sequences, taking sequence 2 from above:
Similar to above, the calculations this time are 1 x 2, 2 x 3, 3 x 4, 4 x 5, or in general n(n+1), if we then compare to the image below:
I am sure there are other uses I haven't yet thought of (I think it may be applicable to geometric and Fibonacci sequences as well, and possibly series at A-Level). When I get chance to explore more I will try and remember to write about it!
P.S. - of course if you have multi-link cubes or similar then pupils can actually build these sequences, graphs etc. as well as just seeing or drawing the pictures.