Recently we have been reviewing the KS3 programme of study in relation to the new KS3 National Curriculum and also how our KS3 programme relates to the changes in the KS2 curriculum to see whether we need to make changes due to overlap. In my perusal of the KS3 curriculum document this phrase jumped out at me:
- move freely between different numerical, algebraic, graphical and diagrammatic representations
- Sequences: 1, 3, 5, 7, 9, 11, ....
- Coordinates: (1, 1), (2, 3), (3, 5), (4, 7), (5, 9), ...
- Table of values 1 2 3 4 5
- Algebraic Sequence notation: Tn = 2n - 1
- Line equation y = 2x - 1
- One-dimensional diagrammatical representation:
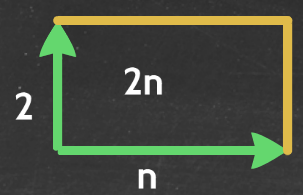
- Two-dimensional diagrammatical representation:
I definitely think it will be interesting to work with pupils and find ways of working with algebra in different representations - choosing a suitable representation for a problem and transferring from one representation to another as the need allows.